ENUNCIADO DEL EJEMPLO 20
Un sólido está formado por un disco homogéneo de espesor despreciable, masa M y radio R, soldado a una varilla rígida sin masa de longitud 2b unida ortogonalmente al disco por el centro O de ambos sólidos. La varilla se apoya por un extremo sobre el suelo liso horizontal, sobre el que puede deslizar libremente.
Cargamos los paquetes de Maple que vamos a emplear.
| > |
with(linalg):with(plots):with(plottools): |
Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined
Warning, the name arrow has been redefined
| > |
libname:="C:\",libname: |
| > |
cg:=[X,Y,psi,theta,phi]; |
![cg := [X, Y, psi, theta, phi]](images/ejemplo20m_1.gif)
Este problema tiene 5 grados de libertad correspondientes a las coordenadas del centro de gravedad del sólido respecto de unos ejes fijos(X, Y), y los tres giros a los que puede estar sometido el mismo: precesión (psi), nutación (theta) y rotación propia (phi). Definiré los elementos del sistema referidos a un sistema de referencia s1 que acompañe al sólido en su movimiento, cuyo centro coincidirá con el centro de gravedad del sistema y los ejes estén ligados al solido de forma que el eje z sigue la direccion de la varilla y los ejes (x,y) est\341n en el plano del disco. Definiré también segmentos como elementos gráficos para simbolizar los ejes del subsistema de referencia, así como los ejes de sistema de referencia de ejes fijos.
| > |
v1:=[varilla,[0,0,0],rota(0,1),0,2*b]: |
| > |
d1:=[disco,[0,0,0],rota(0,1),M,R]: |
| > |
ejeX:=[segmento,[0,0,0],[20,0,0],red]: |
| > |
ejeY:=[segmento,[0,0,0],[0,20,0],green]: |
| > |
ejeZ:=[segmento,[0,0,0],[0,0,20],blue]: |
| > |
TO := [texto,[0,0,-1],"O"]: |
| > |
TY := [texto,[0,20,1],"Y"]: |
| > |
TZ := [texto,[0,0,21],"Z"]: |
| > |
TX := [texto,[20,0,1],"X"]: |
| > |
ejex:=[segmento,[0,0,0],[7,0,0],grey]: |
| > |
ejey:=[segmento,[0,0,0],[0,7,0],grey]: |
| > |
ejez:=[segmento,[0,0,0],[0,0,7],grey]: |
| > |
s1:=[subsistema2,[X,Y,b*cos(theta)],evalm(rota(psi,3)&*rota(theta,1)&*rota(phi,3)),[v1,d1,ejex,ejey,ejez]]: |
| > |
sistema:=[s1,ejeX,ejeY,ejeZ,TO,TY,TX,TZ]: |
Así introducimos unos valores arbitrarios para comprobar si el sistema está bien definido.
| > |
fG([evalf(2),evalf(2),evalf(Pi/4),evalf(Pi/8),evalf(Pi/3)]); |
![[Plot]](images/ejemplo20m_2.gif)
| > |
g:='g':M:='M':b:='b':R:='R': |
De esta forma volvemos a darle un carácter general a los datos para poder desarrollar la Lagrangiana de una forma genérica.
| > |
T:=simplify(fT(sistema)): |
Introducida la Lagrangiana en la variable L, obtenemos las ecuaciones del movimiento.
| > |
ecua:=map(simplify,ec_lag()); |
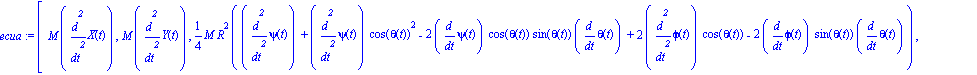
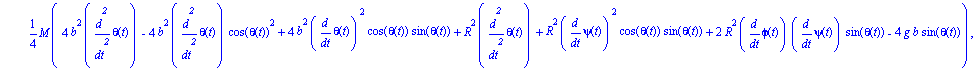

Volvemos a introducirle unos valores arbitrarios a los parámetros para poder realizar la integración numérica, para la cuál es necesario indicar unos valores iniciales de las coordenadas generalizadas y de las velocidades.
| > |
res:=fint([2,30,2,20,evalf(Pi/4),Pi,evalf(Pi/8),Pi,evalf(Pi/3),Pi]): |
Obtenemos una animación del movimiento y las gráficas de las distintas coordenadas generalizadas respecto del tiempo.
![[Plot]](images/ejemplo20m_6.gif)
| > |
odeplot(res,[t,X(t)],0..4.,numpoints=100); |
![[Plot]](images/ejemplo20m_7.gif)
| > |
odeplot(res,[t,Y(t)],0..4.,numpoints=100); |
![[Plot]](images/ejemplo20m_8.gif)
Las coordenadas X e Y son coordenadas cíclicas, su derivada es constante y por lo tanto var\355an linealmente con el tiempo.
| > |
odeplot(res,[t,phi(t)],0..4.,numpoints=100); |
![[Plot]](images/ejemplo20m_9.gif)
| > |
odeplot(res,[t,psi(t)],0..4.,numpoints=100); |
![[Plot]](images/ejemplo20m_10.gif)
| > |
odeplot(res,[t,theta(t)],0..4.,numpoints=100); |
![[Plot]](images/ejemplo20m_11.gif)
![]()
![[Plot]](images/ejemplo20m_2.gif)
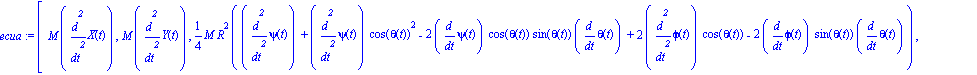
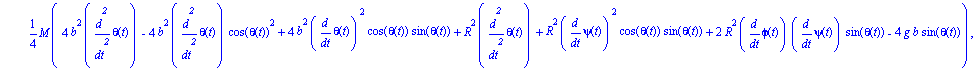

![[Plot]](images/ejemplo20m_6.gif)
![[Plot]](images/ejemplo20m_7.gif)
![[Plot]](images/ejemplo20m_8.gif)
![[Plot]](images/ejemplo20m_9.gif)
![[Plot]](images/ejemplo20m_10.gif)
![[Plot]](images/ejemplo20m_11.gif)