Conceptos generales
La plasticidad computacional tiene por objeto simular los procesos de
deformación de sólidos en los que aparecen deformaciones irreversibles. El
interés de este tipo de simulaciones sigue aumentando dentro de la
ingeniería ya que permite reproducir el comportamiento de materiales como
suelos, rocas, hormigones, metales, etc. en situaciones muy diversas. Como
ejemplo se pueden se√Īalar las correspondientes a los mecanismos de agotamiento
y rotura de elementos estructurales, los procesos de conformado de metales en
los que el efecto de las deformaciones no recuperables est√° controlado y tiene
una finalidad específica, la respuesta estructural a solicitaciones severas
(explosión, impacto), etc.
Para que los an√°lisis de plasticidad con grandes deformaciones sean v√°lidos hay
dos requisitos imprescindibles:
1. Leyes constitutivas que sean físicamente validas y representativas
del fenómeno que se desea representar, para lo cual la cinemática del continuo
elastopl√°stico con grandes deformaciones debe de estar correctamente
descrita
2. Modelos de c√°lculo robustos y computacionalmente eficientes,
para la integración numérica de las ecuaciones de la plasticidad
Asimismo, la modelización de estos problemas lleva asociada dificultades
inherentes al propio tratamiento
numérico:
- bloqueo de la malla en situaciones de flujo plástico isocórico
- problemas de convergencia en situaciones altamente no lineales
- detección y tratamiento adecuado de contactos, ...
e inconvenientes adicionales en el caso en que haya grandes deformaciones:
- elevada distorsión de los elementos
- necesidad de considerar las grandes rotaciones para que los resultados
sean objetivos, etc.
En esta línea de investigación se emplea un modelo hiperelástico basado
en la descomposición multiplicativa del tensor gradiente de deformación
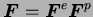 . La configuración intermedia se determina mediante la
actualización multiplicativa del tensor elástico de Finger, y las ecuaciones
de la plasticidad se integran mediante un algoritmo "Euler implícito" para el
retorno a la superficie de fluencia. En el modelo se incluyen como caso
particular los problemas con deformaciones infinitesimales.
. La configuración intermedia se determina mediante la
actualización multiplicativa del tensor elástico de Finger, y las ecuaciones
de la plasticidad se integran mediante un algoritmo "Euler implícito" para el
retorno a la superficie de fluencia. En el modelo se incluyen como caso
particular los problemas con deformaciones infinitesimales.
![[Logo del G.M.C.]](/imagenes/gmc-tiny.png)
![[Escuela T.S. de Ing. de Caminos]](/imagenes/escudoco1.gif) Escuela Ingenieros de Caminos
Escuela Ingenieros de Caminos
![[Universidad Politecnica de Madrid]](/imagenes/upmpeque.gif) Universidad Politécnica de Madrid
Universidad Politécnica de Madrid
![[Logo del G.M.C.]](/imagenes/gmc-tiny.png)

